关于Merge Sort的空间复杂度分析

老师关于归并排序的空间复杂度分析我觉得是O(n)，我是这么分析的：

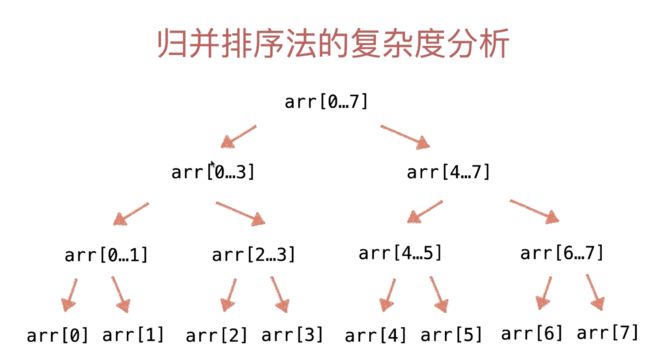
对于递归树第0层我们假设输入数据的规模是O(n)级别：

1. 第一层的call stack上我们开辟了O(n/2)级别的空间；

2. 第二层开辟了O(n/4)级别的空间，一直到最后一层我们开辟的空间是O(1)；

3. 所以一共加起来是：O(n + n/2 + n/4 + ...+ 1) = O(2n - 1) = O(n)

4. 虽然递归树有两侧，但是执行有面那一侧的时候左面的部分已经执行完毕，call stack全部弹出，所以排序过程中占用的最大内存空间还是O(n)级别。

不知道这样的分析正不正确？谢谢老师！

相关截图：