package 树结构;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;
public class BST<E extends Comparable<E>> {
//设置结点,结点的构造方法
private class Node{
public E e;
public Node left;
public Node right;
public Node(E e){
this.e=e;
left=null;
right=null;
}
}
//设置树的根结点,元素个数
private Node root;
private int size;
//树的构造方法
public BST(){
root=null;
size=0;
}
//getSize
public int getSize(){
return size;
}
//isEmpty
public boolean isEmpty(){
return size==0;
}
//树的添加方法
public void add(E e){
if (root==null){
root=new Node(e);
size++;
}
else
add(root,e);
}
public void add(Node node,E e){
if (e.equals(node.e))
return;
else if (e.compareTo(node.e)<0 && node.left == null){
node.left=new Node(e);
size++;
return;
}
else if (e.compareTo(node.e)>0 && node.right == null){
node.right=new Node(e);
size++;
return;
}
if (e.compareTo(node.e)<0){
add(node.left,e);
}
else {
add(node.right,e);
}
}
//树的查询操作
public boolean contains(E e){
return contains(root,e);
}
private boolean contains(Node node,E e){
if (node==null)
return false;
if (e.compareTo(node.e)==0)
return true;
else if (e.compareTo(node.e)<0)
return contains(node.left,e);
else
return contains(node.right,e);
}
//遍历
public void preOrder(){
preOrder(root);
}
private void preOrder(Node node){
if (node == null)
return;
System.out.println(node.e);
preOrder(node.left);
preOrder(node.right);
}
//中序遍历
public void inOrder(){
inOrder(root);
}
private void inOrder(Node node){
if (node == null)
return;
inOrder(node.left);
System.out.println(node.e);
inOrder(node.right);
}
//后序遍历
public void lastOrder(){
lastOrder(root);
}
private void lastOrder(Node node){
if (node == null)
return;
lastOrder(node.left);
lastOrder(node.right);
System.out.println(node.e);
}
//非递归前序遍历
public void preOrderNR(){
Stack<Node> stack=new Stack<Node>();
stack.push(root);
while (!stack.isEmpty()){
Node cur=stack.pop();
System.out.println(cur.e);
if (cur.right != null)
stack.push(cur.right);
if (cur.left != null)
stack.push(cur.left);
}
}
//非递归层序遍历
public void levelOrder(){
Queue<Node> q=new LinkedList<>();
q.add(root);
while (!q.isEmpty()){
Node cur=q.remove();
System.out.println(cur.e);
if (cur.left != null)
q.add(cur.left);
if (cur.right != null)
q.add(cur.right);
}
}
//查询最小元素,
public E minimum(){
if (size==0)
throw new IllegalArgumentException("BST is empty!");
return minimum(root).e;
}
public Node minimum(Node node){
if (node.left == null)
return node;
return minimum(node.left);
}
//查询最大元素,
public E maximum(){
if (size==0)
throw new IllegalArgumentException("BST is empty!");
return maximum(root).e;
}
public Node maximum(Node node){
if (node.right == null)
return node;
return maximum(node.right);
}
// 删除最小元素,
public E removemin(){
E ret = minimum();
removemin(root);
return ret;
}
public Node removemin(Node node){
//这是递归到底的情况,如何去删除
if (node.left==null){
Node nodeRight=node.right;
node.right=null;
size--;
return nodeRight;
}
//这是没有递归到底的情况,如何去返回
node.left=removemin(node.left);
//将一个结点的右子树连接在这个结点左子树的位置上,从而删除左子树
return node;
}
// 删除最大元素
public E removemax(){
E ret = maximum();
removemax(root);
return ret;
}
public Node removemax(Node node){
//这是递归到底的情况,如何去删除
if (node.right==null){
Node nodeLeft=node.left;
node.left=null;
size--;
return nodeLeft;
}
//这是没有递归到底的情况,如何去返回
node.right=removemax(node.right);
//将一个结点的左子树连接在这个结点右子树的位置上,从而删除右子树
return node;
}
//删除任一元素
public void remove(E e){
root=remove(root,e);
}
public Node remove(Node node,E e){
if (node==null)
return null;
if (e.compareTo(node.e)<0) {
node.left = remove(node.left, e);
return node;
}
else if (e.compareTo(node.e)>0) {
node.right = remove(node.right, e);
return node;
}
//e==node.e
else {
if (node.left==null){
Node rightNode=node.right;
node.right=null;
size--;
return rightNode;
}
if (node.right==null){
Node leftNode=node.left;
node.left=null;
size--;
return leftNode;
}
//左右子树都不为空的情况
Node successor = minimum(node.right);
successor.right=removemin(node.right);
successor.left=node.left;
node.left=node.right=null;
return successor;
}
}
@Override
public String toString(){
StringBuilder res=new StringBuilder();
generateBSTString(root,0,res);
return res.toString();
}
private void generateBSTString(Node node, int depth, StringBuilder res) {
if (node==null){
res.append(generateDepthString(depth)+"null\n");
return;
}
res.append(generateDepthString(depth)+node.e+"\n");
generateBSTString(node.left,depth+1,res);
generateBSTString(node.right,depth+1,res);
}
private String generateDepthString(int depth) {
StringBuilder res=new StringBuilder();
for (int i=0;i<depth;i++)
res.append("--");
return res.toString();
}
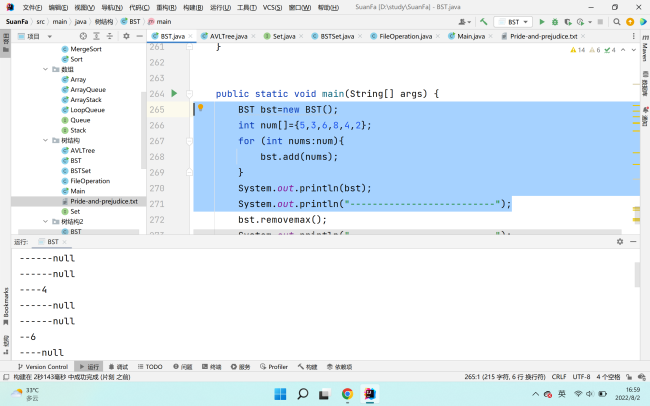
public static void main(String[] args) {
BST<Integer> bst=new BST();
int num[]={5,3,6,8,4,2};
for (int nums:num)
bst.add(nums);
System.out.println(bst);
System.out.println("--------------------------");
bst.removemax();
System.out.println("--------------------------");
System.out.println(bst);
}
}package 树结构;
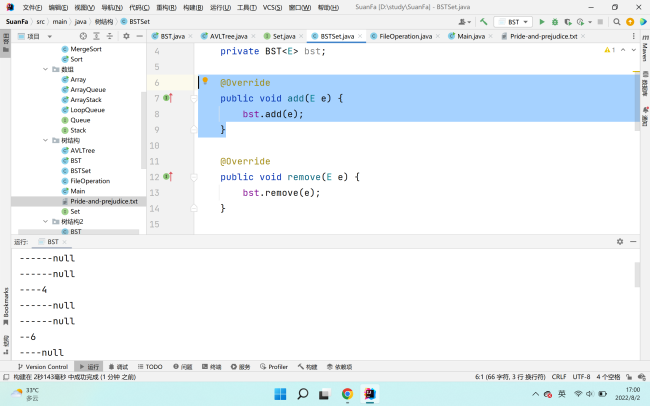
public class BSTSet<E extends Comparable<E>> implements Set<E>{
private BST<E> bst;
@Override
public void add(E e) {
bst.add(e);
}
@Override
public void remove(E e) {
bst.remove(e);
}
@Override
public int getSize() {
return bst.getSize();
}
@Override
public Boolean isEmpty() {
return bst.isEmpty();
}
@Override
public Boolean contains(E e) {
return bst.contains(e);
}
}package 树结构;
import 数组.Array;
import java.util.ArrayList;
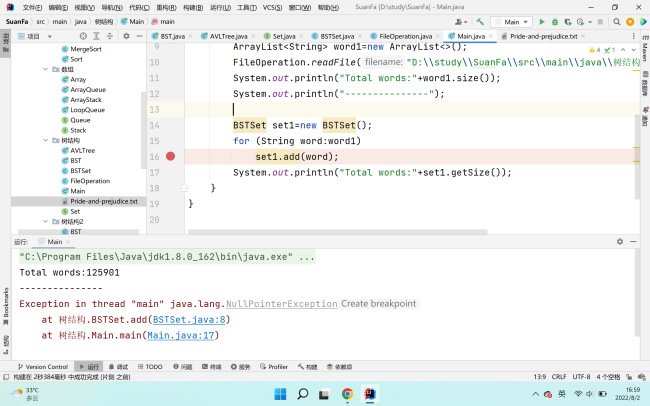
public class Main {
public static void main(String[] args) {
ArrayList<String> word1=new ArrayList<>();
FileOperation.readFile("D:\\study\\SuanFa\\src\\main\\java\\树结构\\Pride-and-prejudice.txt",word1);
System.out.println("Total words:"+word1.size());
System.out.println("---------------");
// BSTSet set1=new BSTSet();
LinkedListSet<String> set2=new LinkedListSet();
for (String word:word1)
set2.add(word);
System.out.println("Total words:"+set2.getSize());
}
}老师这是我两个树类和主方法的代码










恭喜解决一个难题,获得1积分~
来为老师/同学的回答评分吧
0 星