使用numpy对灰度图片进行PCA分解，尝试以列向量为采样数据，还原效果有疑问

开始尝试自己解答，借助DeepsSeek，优化代码后，实现差异很大，找不到原因，需要请教一下。

相关代码：

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.pyplot import imread

img = imread("palomino_horse.png")
img = img[:,:,0] # RGB三通道，200*200*3，三维的值，只去RGB中的一个200*200，并作为灰度值
print(img.shape)

# 使用numpy方式实现
A = img # (200, 200)
# axis=1计算每一行的均值，以列向量作为采样数据(每一列都是不同的变量x,y,z)，行向量作为特征值比如都是x
M = np.mean(A, axis=1, keepdims=True) # keepdims=True是保留维度信息，可deepseek搜索，默认会丢弃维度信息
C = A - M # 中心化，将矩阵A中所有值都减去对应列的期望值 (200, 200)
# 根据公式 Σ=(X^T)X/(n-1)进行计算
V = np.cov(C) # 计算协方差矩阵
# 对协方差进行特征分解
values, vectors = np.linalg.eig(V)
# 对特征值进行降序排列，默认升序排列，返回值翻转，返回对应的索引
sorted_index = np.argsort(values)[::-1]
# 将特征值和特征向量按照索引进行排序
values_sorted = values[sorted_index]
# 注意，特征向量是纵向的列，一个特征值，对应对应列的向量
vectors_sorted = vectors[:,sorted_index]

# 取前60个特征值与对应的特征向量
values = values_sorted[:60]
components = vectors_sorted[:, :60] # 200 * 60

# 投影到主成分空间【案例1】
transformed1 = np.dot(C, components)
# 重构图像
img_new1 = np.dot(transformed1, components.T) + M
# 确保重构后的值在合理范围内
img_new1 = np.clip(img_new1, 0, 255)
plt.imshow(img_new1, cmap='gray') # 灰度展示
plt.show()

# 投影到主成分空间【案例2】
transformed2 = np.dot(components.T, C)
# 重构图像
img_new2 = np.dot(components, transformed2) + M
img_new2 = np.clip(img_new2, 0, 255)
plt.imshow(img_new2, cmap='gray') # 灰度展示
plt.show()

【代码注释中，案例1是按照公式实现的，效果不理想】

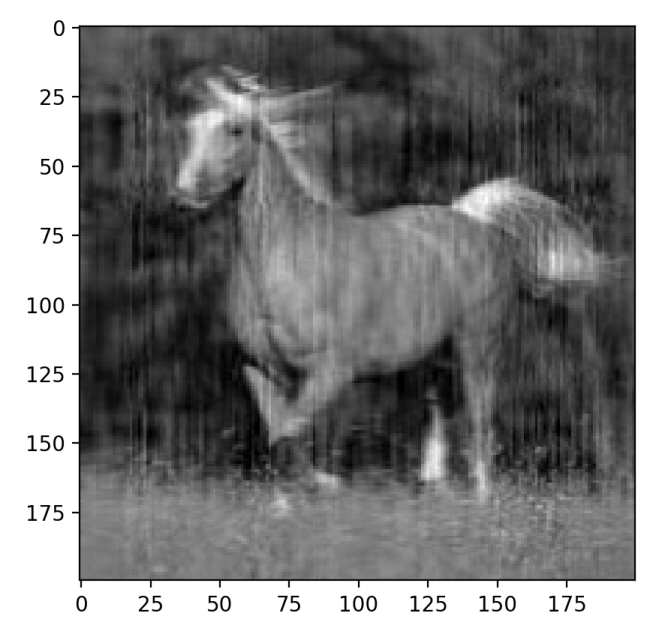
【代码注释中，案例2是参考DeepSeek修改的，效果可以，但不知道为啥，求指教谢谢】

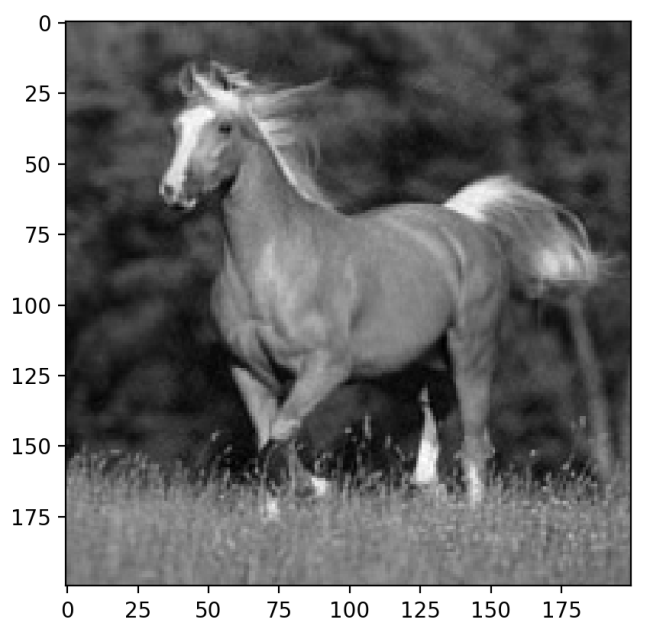
哈哈大圣618 2025-11-05

源自：主成分分析PCA 1-9 PCA主成分分析的练习-4

收起

2回答

GuoSr 2025-11-06 14:15:35

同学，你的代码我跑了一下，发现 case1，case2都有明显的缺陷，如下：

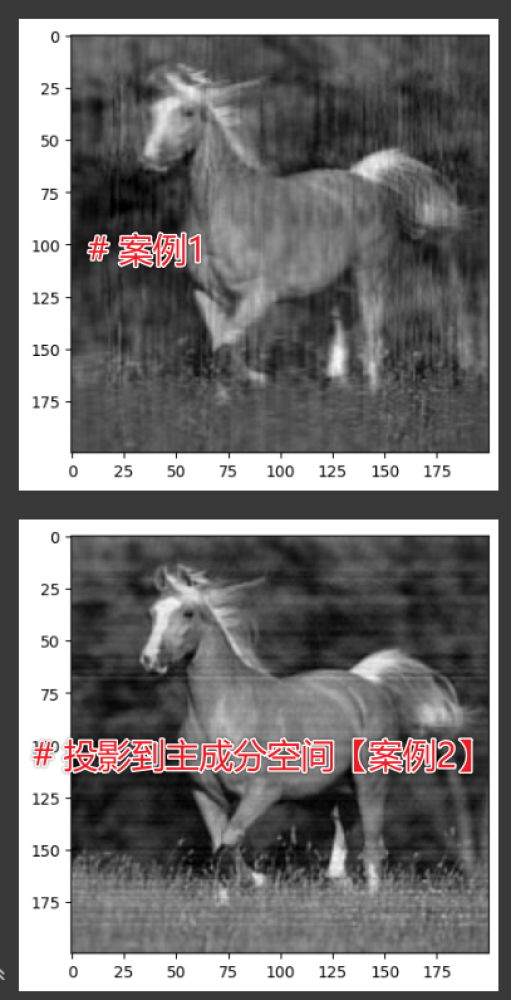
研究了一下，发现问题在于在数据处理的时候，特征与样本的维度被弄混淆了，图片200x200的，每一行看成一个样本，每个样本有200个特征。按照这个思路，将代码如下修改，就会得到比较好的还原效果。

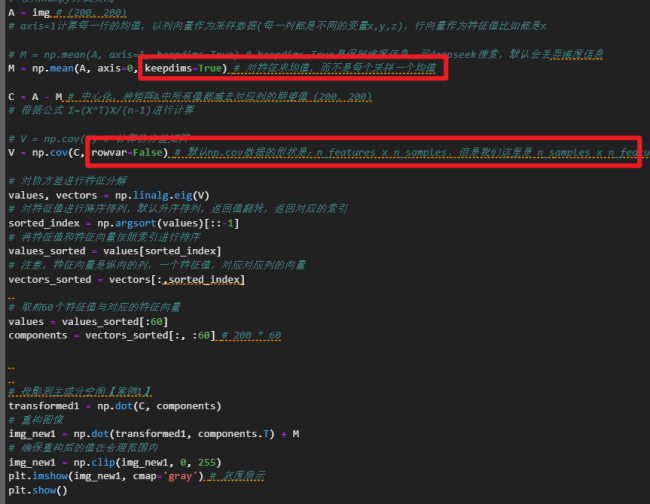
修改后的完整代码如下：

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.pyplot import imread
 
img = imread("palomino_horse.png")
img = img[:,:,0] # RGB三通道，200*200*3，三维的值，只去RGB中的一个200*200，并作为灰度值
print(img.shape)

# 使用numpy方式实现
A = img # (200, 200)
# axis=1计算每一行的均值，以列向量作为采样数据(每一列都是不同的变量x,y,z)，行向量作为特征值比如都是x

# M = np.mean(A, axis=1, keepdims=True) # keepdims=True是保留维度信息，可deepseek搜索，默认会丢弃维度信息
M = np.mean(A, axis=0, keepdims=True) # 对特征求均值，而不是每个采样一个均值

C = A - M # 中心化，将矩阵A中所有值都减去对应列的期望值 (200, 200)
# 根据公式 Σ=(X^T)X/(n-1)进行计算

# V = np.cov(C) # 计算协方差矩阵
V = np.cov(C, rowvar=False) # 默认np.cov数据的形状是：n_features x n_samples，但是我们这里是 n_samples x n_features

# 对协方差进行特征分解
values, vectors = np.linalg.eig(V)
# 对特征值进行降序排列，默认升序排列，返回值翻转，返回对应的索引
sorted_index = np.argsort(values)[::-1]
# 将特征值和特征向量按照索引进行排序
values_sorted = values[sorted_index]
# 注意，特征向量是纵向的列，一个特征值，对应对应列的向量
vectors_sorted = vectors[:,sorted_index]
 
# 取前60个特征值与对应的特征向量
values = values_sorted[:60]
components = vectors_sorted[:, :60] # 200 * 60
 
 
 
# 投影到主成分空间【案例1】
transformed1 = np.dot(C, components)
# 重构图像
img_new1 = np.dot(transformed1, components.T) + M
# 确保重构后的值在合理范围内
img_new1 = np.clip(img_new1, 0, 255)
plt.imshow(img_new1, cmap='gray') # 灰度展示
plt.show()

收起回答

哈哈大圣618 提问者 2025-11-05 08:36:06

思考，需求证对不对：

以行向量作为采样数据(每一列都是不同的变量x,y,z)，列向量作为特征值比如都是x。
中心化的数据如下
x1 y1 z1
x2 y2 z2
x3 y3 z3
特征向量的格式如下，以列的形式
a1 b1 c1
a2 b2 c2
a3 b3 c3
第一个采样数据进行主成分投影的计算比如为。按照投影的计算方式：中心化数据 @ 排序后的主成分矩阵(特征值向量)=投影矩阵
x1a1 + y1a2 + z1a3; 
x2a1 + y2a2 + z2a3; 
x3a1 + y3a2 + z3a3; 
重构图像的公式为：投影矩阵 @ 排序后的主成分矩阵(特征值向量).转置

以列向量作为采样数据(每一列都是不同的变量x,y,z)，行向量作为特征值比如都是x
中心化的数据如下
x1 x2 x3
y1 y2 y3
z1 z2 z3
特征向量的格式如下，以列的形式
a1 b1 c1
a2 b2 c2
a3 b3 c3
如果要保证投影的计算保持不变，需要对投影的计算公式变形：排序后的主成分矩阵(特征值向量).转置 @ 中心化数据=投影矩阵
特征向量转置后如下：
a1 a2 a3
b1 b2 b3
c1 c2 c3
计算后的结果如下：排序后的主成分矩阵(特征值向量).转置 @ 中心化数据=投影矩阵
a1x1 + a2y1 + a3z1; a1x2 + a2y2 + a3z2; a1x3 + a2y3 + a3z3
当要重构图像时，因为转换前为转置，逆操作就是转置的转置，也就是本身，因投影前时左乘，还原逆操作也是左乘
公式也对应变化为：排序后的主成分矩阵(特征值向量) @ 投影矩阵

收起回答