行列式是矩阵所有特征值的乘积示例代码没看懂

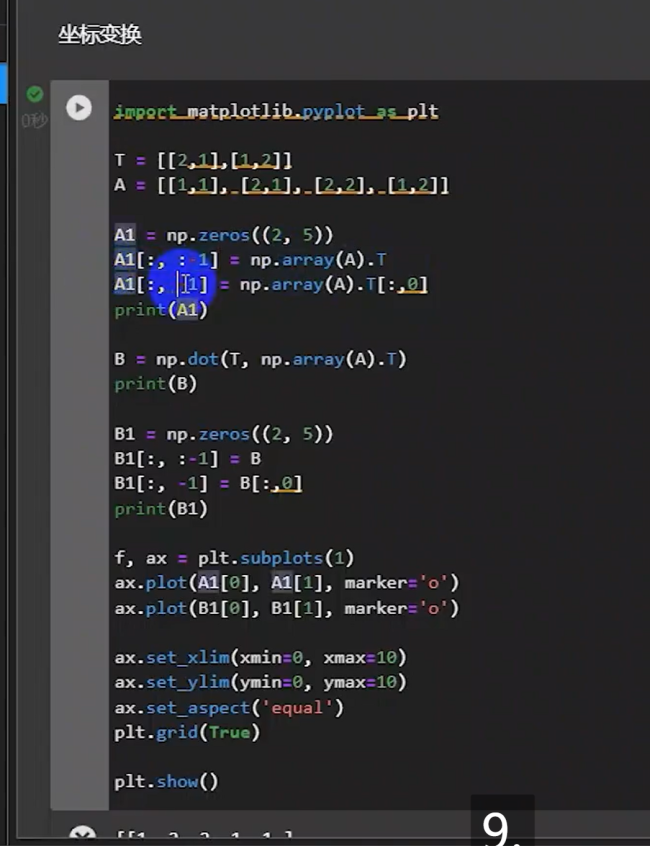
老师，这一段代码有点懵，不知道怎么来的，为什么要这样处理，原理是啥。这里讲的知识点很重要不？如何进行掌握。感觉太跳跃了。

哈哈大圣618 2025-09-05

收起

1回答

慕雪2533642 2025-09-05 23:15:11

这个是 python 的切片 slicing， a1[:,:-1] 这个表示取a1里的所有行所有列除了最后一列同理 b1[:,:-1]这个是取b1 的所有行所有列，然后 b1[:,-1]这个是取b1 的最后一列，大致就讲了有两个矩阵 t ,a 还有一个零矩阵形状是 2行5列的，把a的转置写进0矩阵里除了0矩阵的最后一列，然后把a的转置的第0列写进0矩阵的最后一行，然后再图上画出来 subplot 创建了一个字图返回一个fig(一个画布，所有的子图都在这里) 还有一个子图数组对象ax，因为这里只有一个子图所以直接用ax 调用plt就好了，如果有多个子图可能还要用索引运算符来指定在哪个子图上画，比如plt.subplots(2,2)这里创造了2行2列的子图你想在第一行第二列画就要ax[0,1] (因为是从0索引开始的)

收起回答

提问者哈哈大圣618 #1

感谢，我想知道是背后的数学原理，比如这节课程讲行列式，举例中为什么要这样写，线性变换的步骤为啥是这样，为什么要转置等等，需要具备哪些数学知识，感觉一下上了一个强度，比较跳跃，有点懵。

2025-09-05 23:42:31
GuoSr 回复提问者哈哈大圣618 #2
你好，这就是矩阵对向量进行坐标变换的固定写法，其中并没有高深的数学知识，只是需要用代码反复实验，理解其中的含义。比如用下列代码观察A和A1之间的关系：
```
T = [[2,1],[1,2]]
A = [[1,1], [2,1], [2,2], [1,2]]

print('A\n', np.array(A))
print('\nAT\n', np.array(A).T)

A1 = np.zeros((2, 5))
print('\nA1  0\n', A1)

A1[:, :-1] = np.array(A).T
print('\nA1 1\n', A1)

A1[:, -1] = np.array(A).T[:,0]
print('\nA1 2\n', A1)
```
比如说想知道为什么要转置，你可以实验下面的代码：
```
B = np.dot(T, np.array(A))
print(B)
```
就会发现由于形状的不匹配， T和A不能直接点积，需把A转置后才能符合形状的要求；那为什么需要把A转置？就牵涉到点积，向量，矩阵的定义，线性代数就是设计了这样的一系列符号和运算规则，可以说就是设计成这样的而已。

你也可以先看第六周的“Numpy快速上手”理解numpy的切片等操作。。。
2025-09-06 21:18:33
提问者哈哈大圣618 回复 GuoSr #3

好的，感谢老师

2025-09-08 22:31:33